COVID-19 in Belgium

Introduction
The Novel COVID-19 Coronavirus is still spreading quickly in several countries and it does not seem like it is going to stop anytime soon as the peak has not yet been reached in many countries.
Since the beginning of its expansion, a large number of scientists across the world have been analyzing this Coronavirus from different perspectives and with different technologies with the hope of coming up with a cure in order to stop its expansion and limit its impact on citizens.
Motivations, limitations and structure of the article
By seeing and organizing many R resources about COVID-19, I am fortunate enough to have read a lot of excellent analyses on the disease outbreak, the impact of different health measures, forecasts of the number of cases, projections about the length of the pandemic, hospitals capacity, etc.
Furthermore, I must admit that some countries such as China, South Korea, Italy, Spain, UK and Germany received a lot of attention as shown by the number of analyses done on these countries. However, to my knowledge and at the date of publication of this article, I am not aware of any analysis of the spread of the Coronavirus specifically for Belgium.1 The present article aims at filling that gap.
Throughout my PhD thesis in statistics, my main research interest is about survival analysis applied to cancer patients (more information in the research section of my personal website). I am not an epidemiologist and I have no extensive knowledge in modelling disease outbreaks via epidemiological models.
I usually write articles only about things I consider myself familiar with, mainly statistics and its applications in R. At the time of writing this article, I was however curious where Belgium stands regarding the spread of this virus, I wanted to play with this kind of data in R (which is new to me) and see what comes out.
In order to satisfy my curiosity while not being an expert, in this article I am going to replicate analyses done by more knowledgeable people and apply them to my country, that is, Belgium. From all the analyses I have read so far, I decided to replicate the analyses done by Tim Churches and Prof. Dr. Holger K. von Jouanne-Diedrich. This article is based on a mix of their articles which can be found here and here. They both present a very informative analysis on how to model the outbreak of the Coronavirus and show how contagious it is. Their articles also allowed me to gain an understanding of the topic and in particular an understanding of the most common epidemiological model. I strongly advise interested readers to also read their more recent articles for more advanced analyses and for an even deeper understanding of the spread of the COVID-19 pandemic.
Other more complex analyses are possible and even preferable, but I leave this to experts in this field. Note also that the following analyses take into account only the data until the date of publication of this article, so the results should not be viewed, by default, as current findings.
In the remaining of the article, we first introduce the model which will be used to analyze the Coronavirus outbreak in Belgium. We also briefly discuss and show how to compute an important epidemiological measure, the reproduction number. We then use our model to analyze the outbreak of the disease in the case where there would be no public health intervention. We conclude the article by summarizing more advanced tools and techniques that could be used to further model COVID-19 in Belgium.
Additional considerations
As previously mentioned, the SIR model and the analyses done above are rather simplistic and may not give a true representation of the reality. In the following sections, we highlight five improvements that could be done to enhance theses analyses and lead to a better overview of the spread of the Coronavirus in Belgium.
Ascertainment rates
In the previous analyses and graphs, it is assumed that the number of confirmed cases represent all the cases that are infectious. This is far from reality as only a proportion of all cases are screened, detected and counted in the official figures. This proportion is known as the ascertainment rate.
The ascertainment rate is likely to vary during the course of an outbreak, in particular if testing and screening efforts are increased, or if detections methods are changed. Such changing ascertainment rates can be easily incorporated into the model by using a weighting function for the incidence cases.
In his first article, Tim Churches demonstrates that a fixed ascertainment rates of 20% makes little difference to the modelled outbreak with no intervention, except that it all happens a bit more quickly.
More sophisticated models
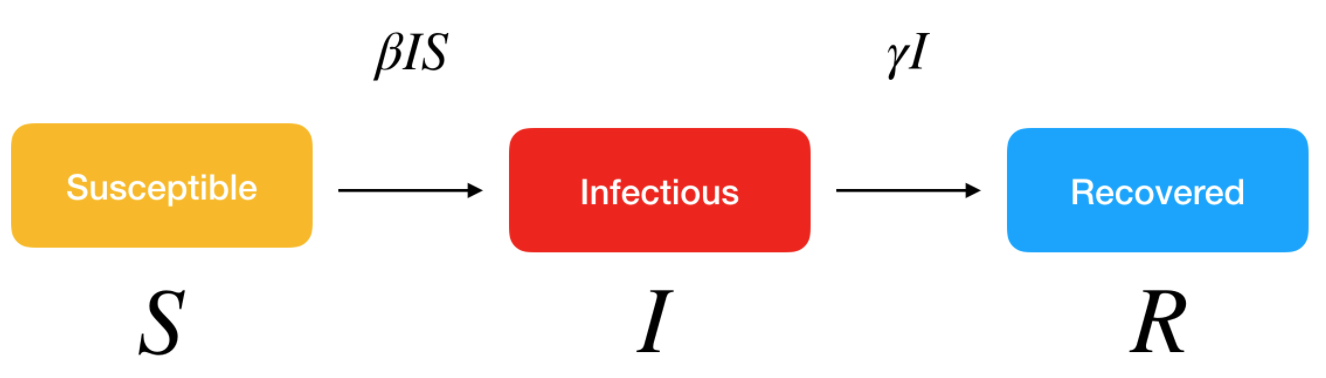
More sophisticated models could also be used to better reflect real-life transmission processes. For instance, another classical model in disease outbreak is the SEIR model. This extended model is similar to the SIR model, where S stands for Susceptible and R stands for Recovered, but the infected people are divided into two compartments:
- E for the Exposed/infected but asymptomatic
- I for the Infected and symptomatic
These models belong to the continuous-time dynamic models that assume fixed transition rates. There are other stochastic models that allow for varying transition rates depending on attributes of individuals, social networking, etc.
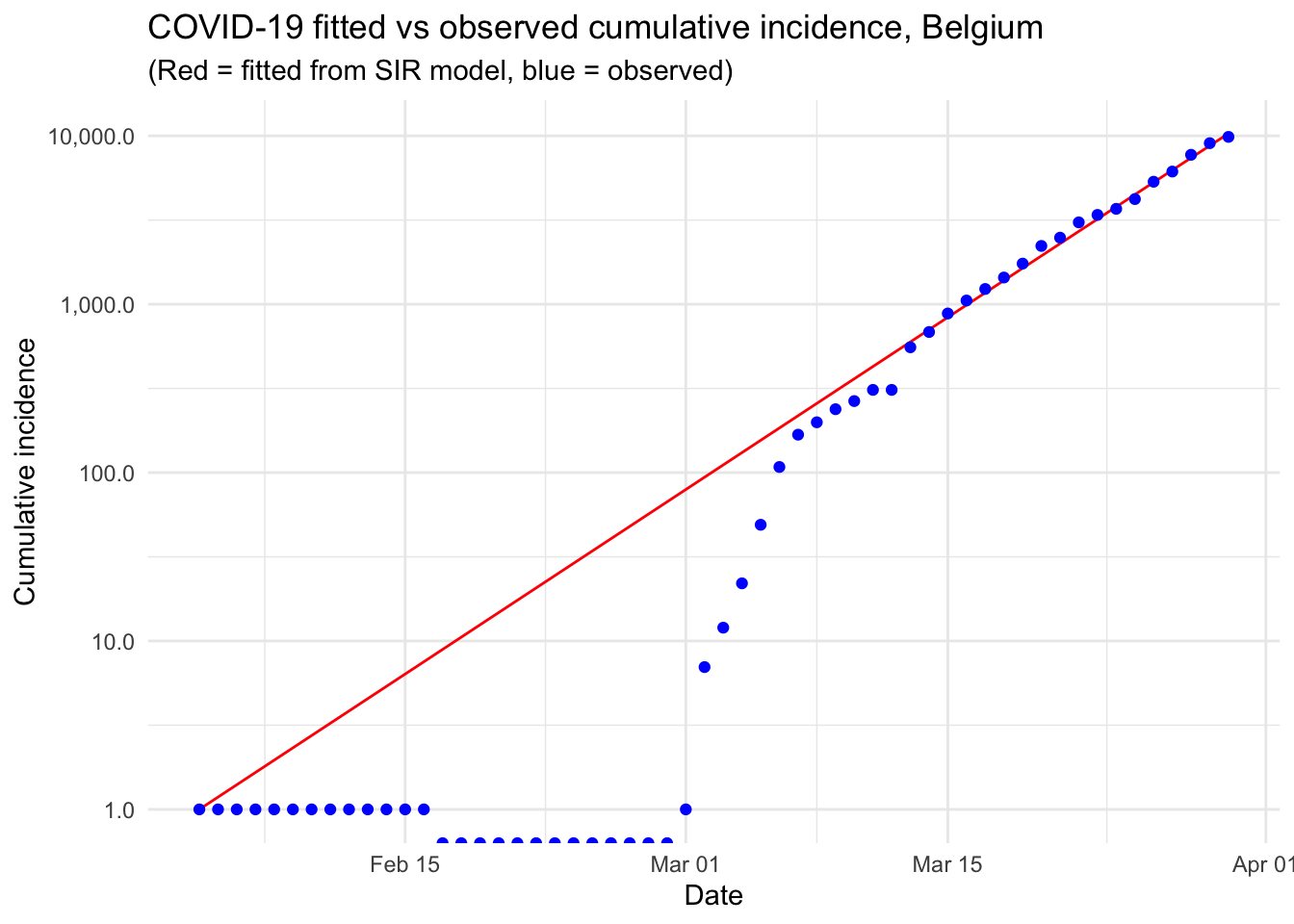
Modelling the epidemic trajectory using log-linear models
As noted above, the initial exponential phase of an outbreak, when shown in a log-linear plot (the y-axis on a log scale and the x-axis without transformation), appears (somewhat) linear. This suggests that we can model epidemic growth, and decay, using a simple log-linear model of the form:
\[log(y)=rt+b\]
where y is the incidence, r is the growth rate, t is the number of days since a specific point in time (typically the start of the outbreak), and b is the intercept. In this context, two log-linear models:
- one to the growth phase (before the peak), and
- one to the decay phase (after the peak)
are fitted to the epidemic (incidence cases) curve.
The doubling and halving time estimates which you very often hear in the news can be estimated from these log-linear models. Furthermore, these log-linear models can also be used on the epidemic trajectory to estimate the reproduction number \(R_0\) in the growth and decay phases of the epidemic.
The {incidence} package in R, part of the R Epidemics Consortium (RECON) suite of packages for epidemic modelling and control, makes the fitting of this kind of models very convenient.
Estimating changes in the effective reproduction number \(R_e\)
In our model, we set a reproduction number \(R_0\) and kept it constant. It would nonetheless be useful to estimate the current effective reproduction number \(R_e\) on a day-by-day basis so as to track the effectiveness of public health interventions, and possibly predict when an incidence curve will start to decrease.
The {EpiEstim} package in R can be used to estimate \(R_e\) and allow to take into consideration human travel from other geographical regions in addition to local transmission (Cori et al. 2013; Thompson et al. 2019).
More sophisticated projections
In addition to naïve predictions based on a simple SIR model, more advanced and complex projections are also possible, notably, with the {projections} package. This packages uses data on daily incidence, the serial interval and the reproduction number to simulate plausible epidemic trajectories and project future incidence.
Conclusion
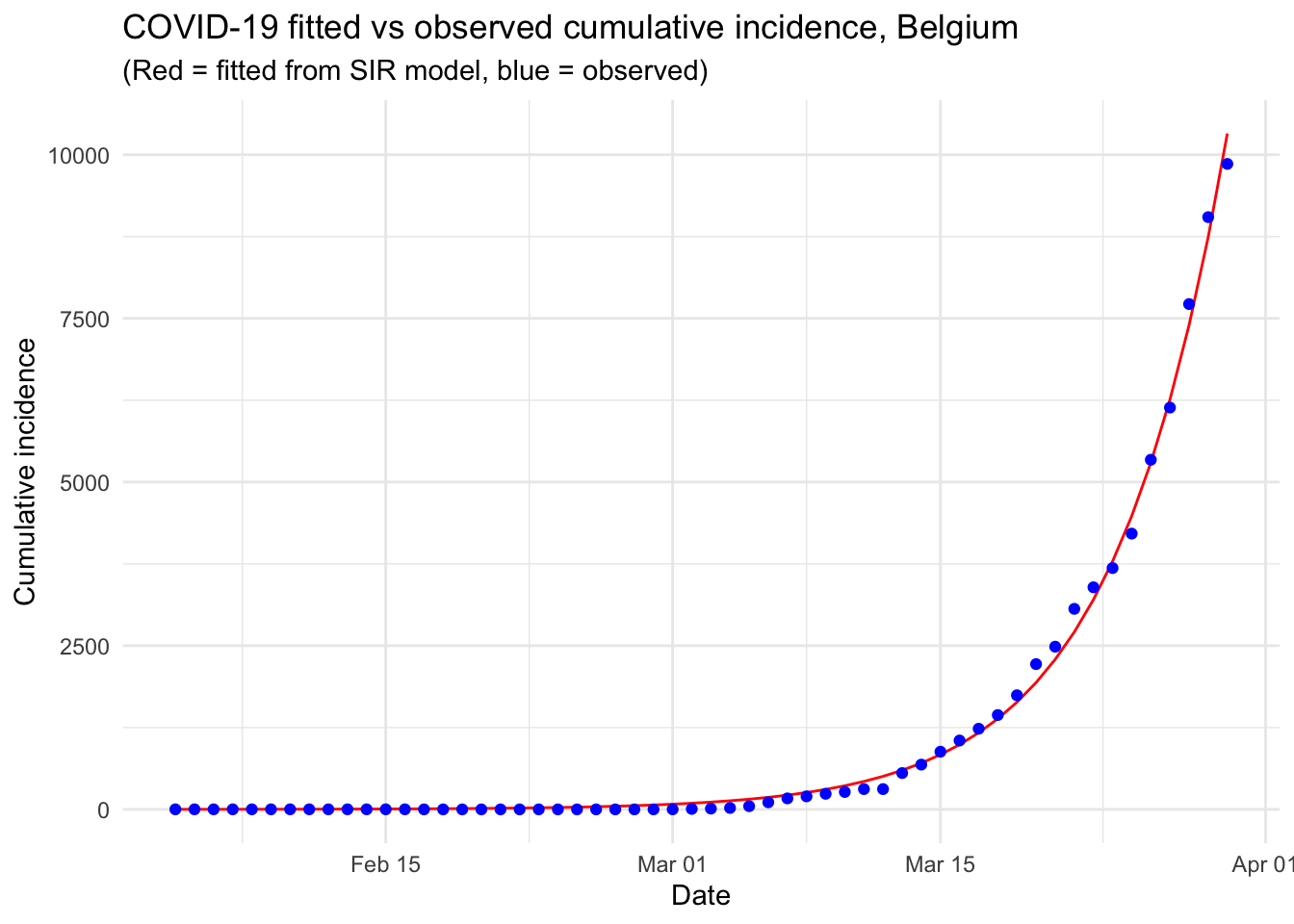
This article started with (i) a description of a couple of R resources on the Coronavirus pandemic (i.e., a collection and a dashboard) that can be used as background materials and (ii) the motivations behind this article. We then detailed the most common epidemiological model, i.e. the SIR model, before actually applying it on Belgium incidence data.
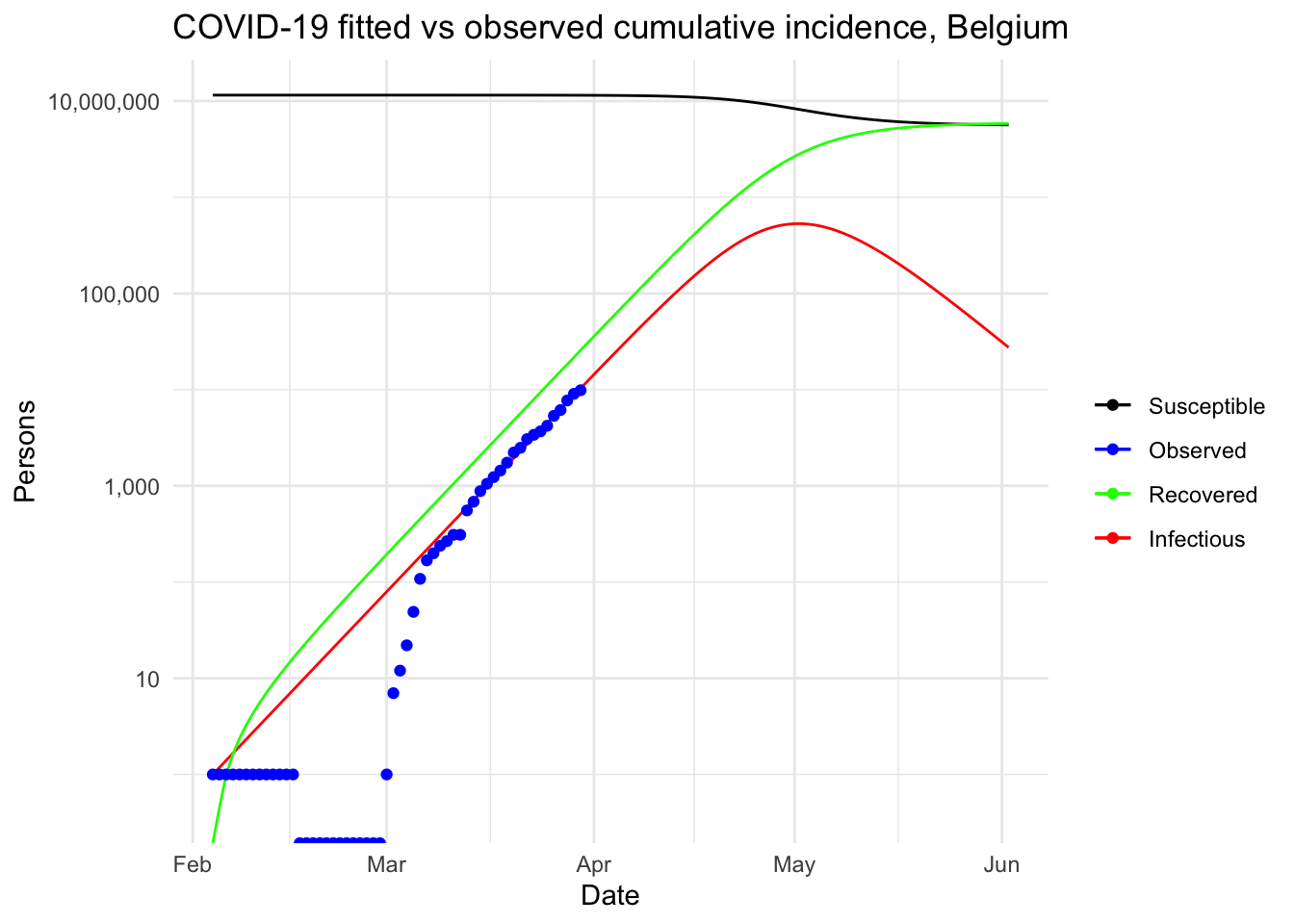
This resulted in a visual comparison of the fitted and observed cumulative incidence in Belgium. It showed that the COVID-19 pandemic is clearly in an exponential phase in Belgium in terms of number of confirmed cases.
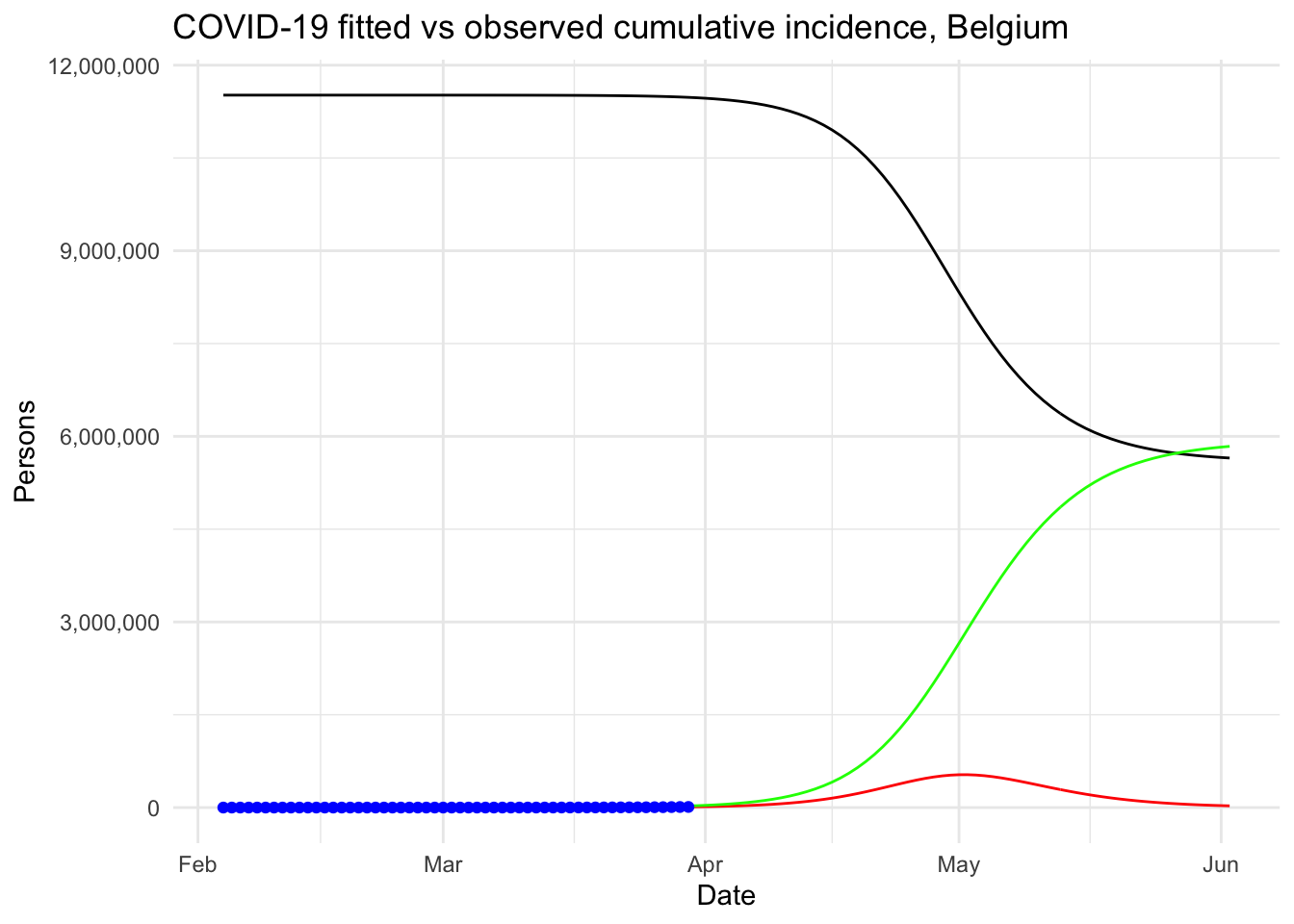
We then explained what is the reproduction number and how to compute it in R. Finally, our model was used to analyze the outbreak of the Coronavirus if there was no public health intervention at all.
Under this (probably too) simplistic scenario, the peak of the COVID-19 in Belgium is expected to be reached by the beginning of May, 2020, with around 530,000 infected people and about 24,000 deaths. These very alarmist naïve predictions highlight the importance of restrictive public health actions taken by governments, and the urgency for citizens to follow these health actions in order to mitigate the spread of the virus in Belgium (or at least slow it enough to allow health care systems to cope with it).
We concluded this article by describing five improvements that could be implemented to further analyze the disease outbreak.
Note that this article has been subject to a talk at UCLouvain.
Thanks for reading. I hope this article gave you a good understanding of the spread of the COVID-19 Coronavirus in Belgium. Feel free to use this article as a starting point for analyzing the outbreak of this disease in your own country.
For the interested readers, see also:
- the evolution of hospital admissions and number of confirmed cases in Belgium
- a collection of top R resources on Coronavirus to gain even further knowledge
As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.
References
Cori, Anne, Neil M Ferguson, Christophe Fraser, and Simon Cauchemez. 2013. “A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics.” American Journal of Epidemiology 178 (9): 1505–12.
Fine, Paul, Ken Eames, and David L Heymann. 2011. “"Herd Immunity": A Rough Guide.” Clinical Infectious Diseases 52 (7): 911–16.
Thompson, RN, JE Stockwin, RD van Gaalen, JA Polonsky, ZN Kamvar, PA Demarsh, E Dahlqwist, et al. 2019. “Improved Inference of Time-Varying Reproduction Numbers During Infectious Disease Outbreaks.” Epidemics 29: 100356.
Feel free to let me know in the comments or by contacting me if you performed some analyses specifically for Belgium and which I could include in my article covering the top R resources on the Coronavirus.↩︎
See a more detailed note on the reproduction number by James Holland Jones if you need a deeper understanding.↩︎
Liked this post?
- Get updates every time a new article is published (no spam and unsubscribe anytime):